
Miskoncepcije Bernoullijevog načela
Autor: John Welch, Cabrillo College Physics Dept.
Uobičajena je ideja: "Brzi tok zraka imat će niži tlak od okolnog mirnog zraka." To se često navodi kao "Bernoullijev učinak."
Ovdje želimo pokazati sljedeće:
- Ova je tvrdnja u suprotnosti s opažanjem i
- To nije rezultat koji predviđa Bernoullijeva jednadžba.
Eksperiment:
Da bismo tvrdnju eksperimentalno provjerili, možemo se poslužiti sljedećim uređajem:

Uređaj s četiri različita završetka manometarskih cijevi spojenih na zajednički spremnik. Pušemo li struju zraka preko vrha svake cijevi (sušilom za kosu ili puhalom za zračnu klupu ili puhalom za lišće) a razinu vode u cijevima koristimo kao mjeru promjene tlaka, pokus pokazuje sljedeće:
- Za golu cijev koja nema na vrhu nikakvu plohu - voda u cijevi se diže, što ukazuje na niži tlak.
- Kod cijevi s ravnom plohom na vrhu - ne primjećuje se promjena tlaka.
- Za cijev s konkavnom plohom na vrhu - tlak raste.
- Za cijevi s konveksnom plohom na vrhu - tlak pada.
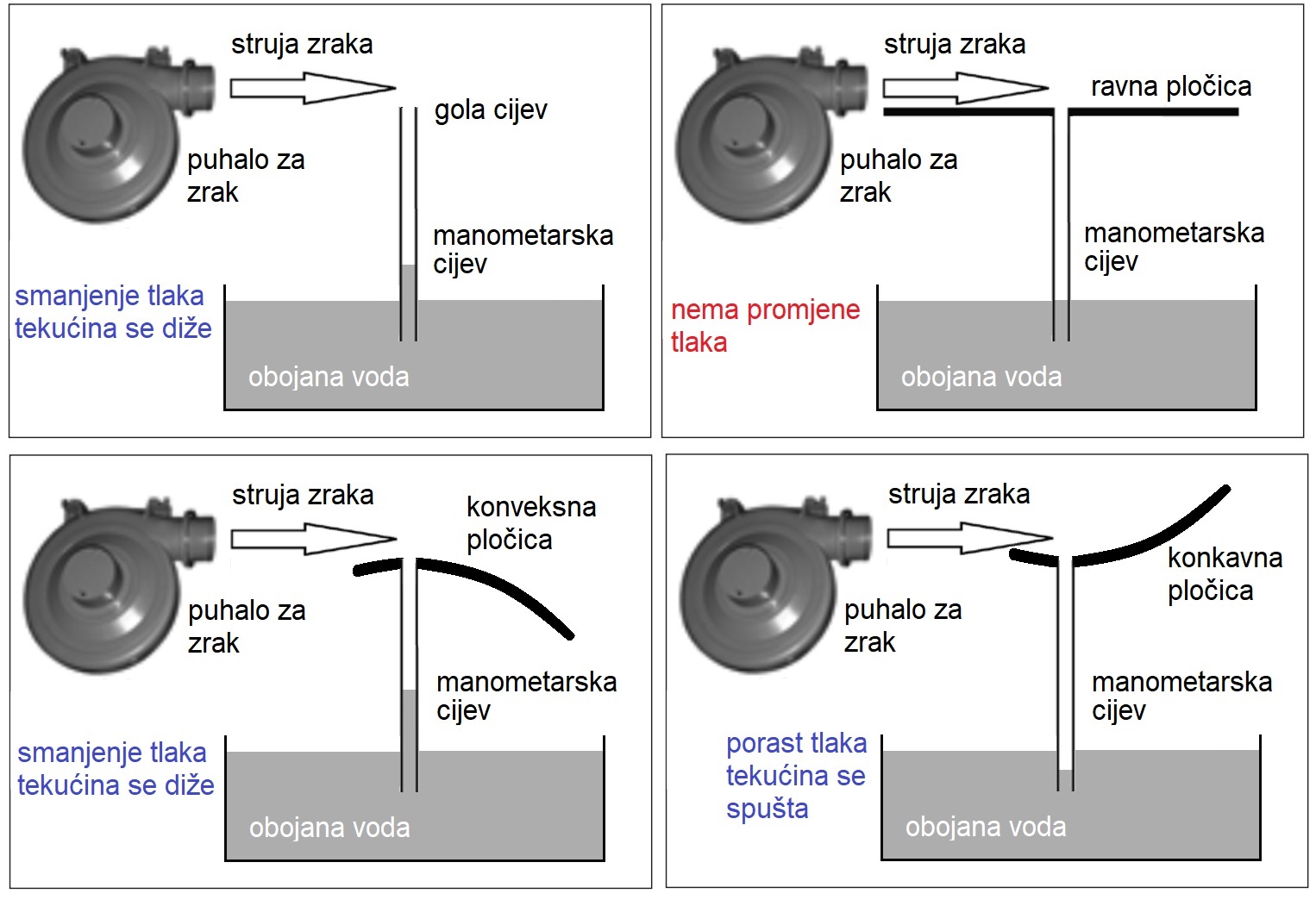
Uočeno je da je tlak u struji zraka koji se brzo kreće isti kao u okolnom zraku, osim ako neka zakrivljena površina ne promijeni njegov smjer. Oblik površine je važna varijabla u određivanju tlaka u struji, a učinak će biti veći kako brzina raste.
Opširnije je pokus objašnjen u člancima:
"Pogrešna primjena Bernoullijevog načela" (na engleskom)
"Pogrešna tumačenja Bernoullijevog zakona" (na engleskom)
Evo i video zapisa s još nekoliko pokusa koji testiraju ideju da "zrak koji brže struji ima niži tlak."
Teorija:
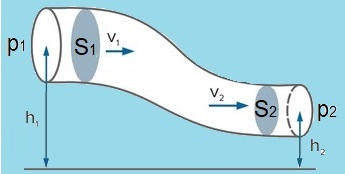
Bernoullijevo načelo je izjava o očuvanju energije mase tekućine u različitim točkama duž njenog toka. On uspoređuje tlak, brzinu i visinu fluida u točkama 1 i 2, koje su duž istog toka. Procjena je da ako vanjske sile ne izvrše rad na promatrani mali volumen tekućine, energija tog dijela tekućine ostat će konstantna.
Ovdje je mahanička analogija:
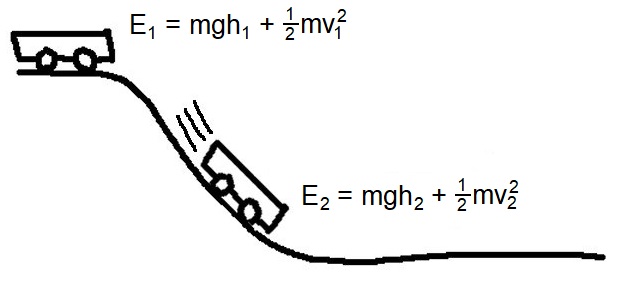
Ako kolica krenu iz mirovanja na vrhu staze, a potom povećavaju brzinu i kinetičku energiju, znamo da pri tome moraju izgubiti gravitacijsku potencijalnu energiju, zar ne? Možemo li onda tvrditi otprilike sljedeće: "kolica na nižoj visini će biti brža?"
Odgovor je: Da, ali pod jednim uvjetom ... Pod uvjetom da vanjske sile ne izvrše nikakav rad na kolicima. Ako kolica poguramo rukom ili motorom, ona očito mogu dobiti kinetičku energiju (KE) bez potrebe da izgube gravitacijsku potencijalnu energiju (GPE), a mogla bi ubrzati čak i na ravnoj stazi.
Bernoullijeva jednadžba je ista stvar za tekućine:
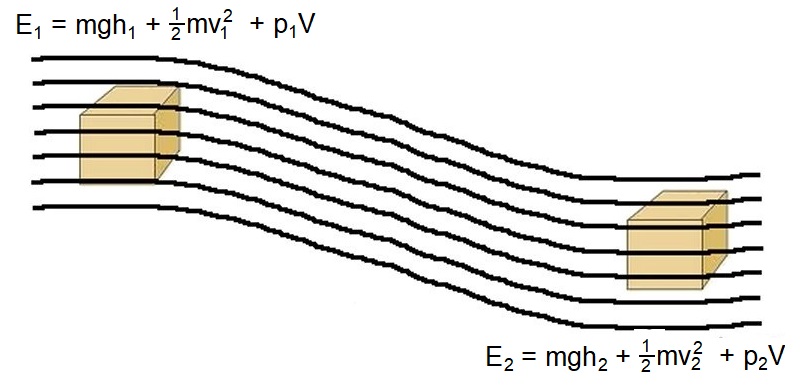
Ovdje razmatramo neki volumen tekućine koja se giba duž strujnica. Postoje tri oblika energije koja taj volumen može imati: gravitacijska potencijalna (mgh), kinetička (1/2 mv2) i unutarnja energija od toga što je "pod tlakom" (pV).
Bernoullijeva jednadžba se obično piše kao zbroj energija po jedinici volumena umjesto energija malog dijela mase: (svaki član podijeljen sa V ⇒ m/V = ρ)
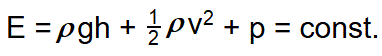
Ako je energija očuvana, i vanjske sile ne vrše rad, tada ako mali volumen tekućine povećava svoju kinetičku energiju, mora mu se smanjiti neki drugi oblik energije. Ako ostane na istoj visini, tada se njegova unutarnja energija, a time i njegov tlak, moraju smanjivati. Pravilo za ovo otprilike glasi "zrak koji se brzo kreće imat će niži tlak." I to vrijedi za strujanje fluida u cijevi. Zato objašnjenje smanjenja tlaka uslijed veće brzine strujanja preko Bernoullijevog očuvanja energije stvara brojne miskoncepcije. Energija je skalar i ne razlikuje smjer djelovanja sile pri skretanju strujnica. Iz tog se razloga Bernoullijevo načelo u pravilu ilustrira protokom fluida u cijevi.
ALI... ako postoji vanjska sila (poput ventilatora) koja vrši rad na mali volumen fluida, ta sila sigurno može izazvati povećanje kinetičke energije (KE) tog dijela, bez ikakvog potrebnog smanjenja visine (GPE) ili tlaka (unutarnja energija - pV) da bi zbroj ostao konstantan kao što kaže Bernoullijevo načelo.
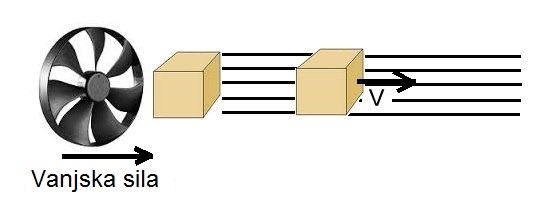
Naše pravilo više ne vrijedi. U ovom slučaju lako bismo mogli imati djelić zraka (ili drugog fluida) koji se brzo kreće i koji je pod istim tlakom kao i okolni mirujući zrak bez ikakvog kršenja očuvanja energije. A budući da je ovaj djelić zraka u kontaktu s okolnim zrakom, ima smisla smatrati da bi tlakovi bili jednaki. To je zapravo ono što se uočava u gornjem eksperimentu s ravnom plohom na vrhu cijevi, kada zrak ne mijenja smjer, odnosno nema izobličenja strujnica.
 Vrijedi li ovo pravilo za krila aviona?
Vrijedi li ovo pravilo za krila aviona?
Budući da se relativna brzina strujanja uz krilo održava na račun izgaranja goriva za pogon motora, imamo situaciju s vanjskim silama, stoga očuvanje energije (E) ne zahtijeva da zrak na vrhu krila bude niži od atmosferskog tlaka. Znamo i da avioni od papira mogu letjeti s ravninskim krilima, odakle slijedi da je profil avionskog krila koristan za ekonomičnu potrošnju goriva, ali nije nužan uvjet za sam let. Uostalom na aero-mitinzima piloti često izvode akrobacije leteći s avionom okrenutim naopako.
Pa što je to što uzrokuje silu podizanja?
Kratki je odgovor da će, ako objekt na bilo koji način preusmjeri zrak, na njega djelovati rezultantna sila prema gore, prema Newtonovom trećem zakonu. To čini 100% silu dizanja. (Jednostavno mora, osim ako ne krši N-ov 3. zakon). Mikroskopski mehanizam pomoću kojeg zakrivljeni vrh krila preusmjerava zrak prema dolje je složen. često se naziva Koanda efektom.
Učenicima možemo objasniti da podizanje proizlazi iz 3. Newtonovog zakona - tj. ako krilo "djeluje" na struju zraka prema dolje ukupnom silom (F = dp/dt), uzrokujući da se ona preusmjeri, tada na krilo mora djelovati odgovarajuća sila prema gore. Ali to obično nije zadovoljavajuće, jer ne objašnjava izvore sila. Zato je Coanda učinak dobar opis onoga što se događa kako bi se uspostavile ove sile. Dok zrak struji preko krila (ili bilo koje zakrivljene površine), on povlači dio obližnjeg zraka sa sobom, stvarajući tako trenutnu 'prazninu' na stražnjoj strani krivulje. I zračni tok i objekt gurani su u tu zavjetrinu okolnom atmosferom, uzrokujući tako istodobno i dizanje krila i skretanje struje zraka.
Zaključak:
Ako je sve tako kako smo rekli, onda moramo zaključiti da smanjenje tlaka nije posljedica povećanja brzine strujanja nego upravo obrnuto. Krivina zapreke oko koje struji fluid stvara područje nižeg tlaka. Čestice fluida se ubrzavaju prema tom području tj. brzina im se povećava zato što je došlo do smanjenja tlaka oko i iza zapreke. Smanjenje tlaka je uzrok povećanja brzine strujanja a ne posljedica. Tamo gdje se strujnice savijaju postoji gradijent tlaka, a uz ravnu površinu tlak se ne mijenja.
Ova animacija nastoji ilustrirati Coanda učinak:
S engleskog preveo:
Hrvoje Mesić
